
文章目录
本文为译文,感谢原作者Weng, Lilian无私的分享。文章原文地址为:https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html
摘要:在本文中,我们深入了解一下策略梯度算法、工作原理以及一些近年来新提出的改进算法,包含:朴素(vanilla)策略梯度、actor-critic、off-policy 策略梯度、A3C、A2C、DPG、DDPG、D4PG、MADDPG、TRPO、PPO、ACER、ACTKR、SAC、TD3以及SVPG。
什么是策略梯度
策略梯度是解决强化学习问题的一类方法。如果您对强化学习领域还不了解,可以先阅读这一篇博文《深入了解深度学习:核心概念》来了解一下基本问题定义以及一些核心概念。
符号
下表列出了一些符号说明,用于帮助更好地理解本文。
| 符号 | 含义 |
|---|---|
| $s\in \mathcal{S}$ | 状态 |
| $a\in \mathcal{A}$ | 行为、动作 (actions) |
| $r\in \mathcal{R}$ | 奖励 (rewards) |
| $S_t, A_t, R_t$ | 一条样本采样/运行路径上时刻$t$时的状态、行为、奖励。文中有时也会使用$s_t, a_t, r_t$ |
| $\gamma$ | 衰减系数;用于对未来不确定性的惩罚;$0 \lt \gamma \le 1$ |
| $G_t$ | 收益;或带衰减的收益:$G_t = \sum_{k=0}^{\infty} \gamma^{k}R_{t+k+1}$ |
| $P(s^{\prime}, r\vert s, a)$ | 在状态$s$下执行行为$a$后,得到的奖励为$r$,并且进入状态$s^\prime$的转移概率 |
| $\pi(a\vert s)$ | 随机策略(执行代理(agent)的行为策略);$\pi_{\theta}(\cdot)$是带参数$\theta$的策略 |
| $\mu(s)$ | 确定性策略;我们也可以使用$\pi(s)$,但是使用符号$\mu$可以让我们更容易区分随机性策略和确定性策略。$\pi$和$\mu$都是在强化学习算法训练过程中学习的 |
| $V(s)$ | 状态价值函数、用于评估状态$s$下的期望收益;$V_w(\cdot)$表示价值函数的参数为$w$ |
| $V^{\pi}(s)$ | 在服从策略$\pi$的情况下状态$s$的期望价值/收益 |
| $Q(s, a)$ | 行为价值函数,和$V(s)$类似,但是其评估的是状态和行为对$(s, a)$的期望收益;$Q_{w} (\cdot)$表示$Q$函数由参数$w$决定 |
| $Q^{\pi} (s, a)$ | 和$V^{\pi} (\cdot)$类似,但是$Q(s, a)$服从策略$\pi$;$Q^{\pi}(s, a) = E_{a \sim \pi}[G_t\vert S_t=s, A_t=a]$ |
| $A(s, a)$ | 优势函数$A(s, a) = Q(s, a) - V(s)$;其可以被看作是另外一种形式的Q值函数,但其以值函数$V$作为基线,大大降低了方差(variance) |
策略梯度
强化学习的目标是找到一个可以让执行代理(agent)获取最大收益的最优策略。而策略梯度算法着眼点在于直接对策略本身进行建模和优化。策略通常用一个带参数(通常用$\theta$表示)的函数来建模。而后,可以使用各种各样的算法来对参数$\theta$进行优化,以达到收益(目标函数)最大化的目标。
收益(目标)函数定义为:
其中$d^{\pi}(s)$为由$\pi_{\theta}$决定的马尔可夫平稳分布(在策略$\pi$下,一个on-policy的状态分布)。为了简化,当策略$\pi_{\theta}$被用作其它函数的下标(或上标)时,参数$\theta$通常会被省略。比如$d^{\pi}, Q^{\pi}$应该指的是$d^{\pi_{\theta}}, Q^{\pi_{\theta}}$。
想象一下,如果你可以持续永久遍历马尔可夫链中的所有状态,那么随着时间的推移,最终你停留在某个状态的概率是一定的,这就是策略$\pi_{\theta}$的平稳性。$d^{\pi}(s)=\lim _{t\to \infty} P(s_t=s|s_0,\pi_\theta)$是从初始状态$s_0$开始,在遵从策略$\pi_{\theta}$的情况下,执行$t$步后,状态停留在$s$的概率。事实上,马尔可夫链的平稳性是$PageRank$算法能够工作的主要原因之一。如果你想了解更多,可以查看这里。
由于在连续空间下,行为或者状态的数量是无限的,基于值(value)的方法的计算代价太大了。举例来说,在一般策略迭代方法中,策略改进那一步$\arg \max_{a\in \mathcal{A}}Q^{\pi}(s, a)$要求对行为空间进行遍历,这就导致了维度诅咒问题。自然而然地,我们会希望基于策略的方法在连续空间中会比策略迭代法更加有用。
根据目标函数的梯度$\nabla_\theta J(\theta)$,我们可以使用策略提升算法,将参数$\theta$往某个特定的方向移动,以使策略$\pi_{\theta}$可以最大化最终收益。
策略梯度定理
计算梯度$\nabla_\theta J(\theta)$是比较棘手的。因为它不仅依赖于行为的选择(由策略$\pi_{\theta}$决定),而且依赖于状态分布的平稳性。而这个状态分布本身还由策略$\pi_\theta$间接的决定。在给定一个未知环境的情况下,很难预测一次策略更新会对状态分布产生什么样的影响。
幸运的是,策略梯度定理出来拯救世界了!鼓掌!它给出了目标函数导数的另外一种简化形式,其中并不包含状态分布$d^{\pi} (\cdot)$。这大大简化了梯度$\nabla_\theta J(\theta)$的计算:
策略梯度定理的证明
本小节信息量较大,是时候来复习一遍证明过程了(Sutton & Barto, 2017,章节13.1),这可以帮助我们了解为什么策略梯度定理是正确的。
我们从对状态价值函数求导开始:
因此,我们有:
这个等式有一个非常漂亮的递归形式(看红色部分!),未来状态的价值函数可以通过同样的形式展开。
考虑如下序列,我们使用$\rho^\pi(s \to x, k)$表示在策略$\pi_{\theta}$指导下,从状态$s$到状态$x$的$k$步转移概率。
我们有:
- $k=0$时,$\rho^\pi (s\to s, k=0) = 1$
- $k=1$时,我们将能够转移到状态$s^\prime$所有可能的行为出现的概率相加得到:$\rho^\pi(s \to s', k=1) = \sum_a \pi_\theta(a \vert s) P(s' \vert s, a)$
- 假设我们的目标是依照策略$\pi_\theta$,从状态$s$经过$k+1$步转移到状态$x$,那么我们可以先从状态$s$经过$k$步转移到状态$s^\prime$,然后再从状态$s^\prime$经过1步转移到状态$x$。通过此种递归的方式,我们拆分转移概率:$\rho^\pi(s \to x, k+1) = \sum_{s'} \rho^\pi(s \to s', k) \rho^\pi(s' \to x, 1)$
回到前面,我们对价值函数的梯度$\nabla_{\theta}V^{\pi}(s)$进行展开。为了简化表示,我们令$\phi(s) = \sum_{a \in \mathcal{A}} \nabla_\theta \pi_\theta(a \vert s)Q^\pi(s, a)$。随着我们对价值函数梯度$\nabla V_\theta(\cdot)$的不断展开,我们可以发现:我们可以从起始状态$s$开始,通过$t$步执行之后,转移到任意一个状态。$\nabla_{\theta} V^\pi$展开如下:
我们将价值函数梯度表示带入到目标函数的公式中,并整理可以得到:
上式中$\propto$表示正比于,在离散的情况下(episodic case),比例系数常量$\sum_s \eta(s)$大小为每一轮(episode)的平均长度。在连续情况下该常量为1(Suton & Barto, 2017;章节13.2)。我们将上面的梯度进一步整理为如下形式:
其中$\mathbb{E}_\pi$表示$\mathbb{E}_{s \sim d_\pi, a \sim \pi_\theta}$,也就是状态和行为分布都遵从策略$\pi_\theta$(on-policy)。
策略梯度定理是许多策略梯度算法的理论基础。这种朴素的策略梯度更新方法是无偏的(bias),但是存在很大的方差(variance)。下面我们提到的许多算法都是为了在保证偏差不变的情况下降低方差而提出的。
这里列出策略梯度算法的一些常用的形式(论文GAE中给出的),这篇文章讨论了GAE中的一些组成部分,强烈推荐。
译著: GAE 这篇文章我们之前有介绍过,参考链接。
GAE 中策略梯度公式简介
策略梯度的公式,通常有如下形式:
其中,$\Psi_t$的形式可以是:
其中,值函数:
Q函数:
优势函数:
策略梯度算法
近年来大量梯度策略算法被提出来,本文不可能介绍所有的算法,这里仅介绍一些我偶然了解到并且读过的一些。
REINFORCE
REINFORCE(蒙特卡洛策略梯度)算法依赖于蒙特卡洛方法生成样本来估计期望收益,以更新策略的参数。由于使用蒙特卡洛方法得到的梯度在期望意义上与实际的梯度是相等的,因此REINFORCE可以正常工作:
我们可以通过实际采样得到的样本路径(sample trajectories)中来估计$G_t$,并使用$G_t$进行策略梯度的参数更新。该方法依赖于完整的样本路径,这也是为什么我们称它是蒙特卡洛方法的原因。
此方法工作过程非常直观:
- 随机初始化策略参数$\theta$
- 使用策略$\pi_\theta$来生成一个样本路径:$S_1, A_1, R_2, S_2, A_2, \ldots, S_T$
- For t = 1, 2, ... , T:
- 估计回报$G_t$的值
- 更新策略参数:$\theta \leftarrow \theta + \alpha \gamma^t G_t \nabla_\theta \ln \pi_\theta(A_t \vert S_t)$
REINFORCE 算法的一个常用变体是将$G_t$减去一个基线值。这样做可以降低梯度估计的方差,并且可以保持偏差不变(记住:我们总是希望执行将$G_t$减去一个基线值这个动作)。举例来说,一个常用的方法就是使用行为价值(action value)函数减去状态价值(state value)函数,也就是使用优势函数$A(s, a) = Q(s, a) - V(s)$来进行参数更新。这篇文章很好地解释了为什么使用基线值可降低方差,其中还介绍了策略梯度算法的一些基础知识。
Actor-Critic
策略梯度中有两个重要组成部分:策略模型和价值函数。除了学习策略之外,学习价值函数也是非常有意义的,因为值函数可以协助梯度更新。举例来说,在朴素策略梯度算法中,我们使用状态价值函数作为基线值时可以降低梯度方差,这就是Actor-Critic所做的事。
Actor-Critic方法由两个模型组成,它们之间可能会共享参数:
- Critic更新价值函数的参数$w$,根据不同的算法,价值函数可以是行为价值函数$Q_w(a,s)$或者状态价值函数$V_w(s)$
- Actor负责更新策略$\pi_\theta (a|s)$的参数$\theta$(使用cirtic指示的方向)
我们来看一下简单的基于行为价值函数的Actor-Critic算法的工作流程:
- 随机初始化$s, \theta, w$;对行为进行采样$a\sim \pi_\theta(a|s)$
- For t = 1, ..., T:
- 采样奖励$r_t \sim R(s, a)$以及下一个状态$s^\prime \sim P(s^\prime|s, a)$
- 采样下一个行为$a^\prime \sim \pi_\theta(a^\prime|s^\prime)$
- 更新梯度参数:$\theta \leftarrow \theta + \alpha_\theta Q_w(s, a) \nabla_\theta \ln \pi_\theta(a \vert s)$
- 计算时刻$t$时的TD值:$\delta_t = r_t + \gamma Q_w(s', a') - Q_w(s, a)$
- 更新行为价值函数的参数:$w \leftarrow w + \alpha_w \delta_t \nabla_w Q_w(s, a)$
- 更新行为与状态:$a\leftarrow a^\prime, s \leftarrow s^\prime$
上面的流程中$\alpha_\theta$和$\alpha_w$是针对策略与价值函数分别预先设置的超参数。
Off-Policy 策略梯度
REINFORCE和actor-critic算法的原始版本都是on-policy的:训练样本都是根据目标策略(target policy)来收集的 (这里目标策略指的是我们正在优化的策略完全一样的策略)。Off-policy方法相比于on-policy的方法有几个优势:
- off-policy方法不要求有一个完整的样本路径它可以重用之前采样得到的样本(经验回放),这样样本采样效率就非常高,数据使用效率也就非常高
- 使用与目标策略不一样的行为策略(behavior policy)来进行采样可以更好的进行探索(exploration)
译著:这里behavior也翻译为了行为,文中我们将 action 也译为了行为,注意区分。
现在让我们看看off-policy的策略梯度是如何计算的。收集样本所用的行为策略是一个已知的策略,用符号$\beta(a|s)$表示。目标函数将行为策略生成的样本所得奖励进行求和:
其中$d^\beta(s)$是行为策略$\beta$的一个平稳分布,$d^\beta(s) = \lim_{t \to \infty} P(S_t = s \vert S_0, \beta)$;$Q^\pi$是根据目标策略(而不是采样所用的行为策略)得到的行为价值函数的估计。
给定根据行为策略所得到的训练观测样本,我们将梯度的形式修改为:
上式中$\cfrac{\pi_\theta (a|s)}{\beta (a|s)}为$重要性权重。由于$Q^\pi$是目标策略的函数,所以$Q^\pi$也是策略参数$\theta$的函数。那么,根据乘法求导法则,我们也需要计算梯度$\nabla_\theta Q^\pi(s, a)$。但实际上,梯度$\nabla_\theta Q^\pi (s, a)$的计算极其困难。幸运的是,我们如果使用将$\nabla_\theta Q$部分忽略的近似梯度,仍然可以保证策略的改进,并且最终可以得到一个局部最优的策略。具体可以参考此处的证明。
简单总结,在off-policy的设定下使用策略梯度算法,我们仅需要对价值函数进行加权求和,权重就是目标策略与行为策略之比:$\frac{\pi_\theta(a \vert s)}{\beta(a \vert s)}$。
A3C
A3C (Asynchronous Advantage Actor-Critic)是一个经典的策略梯度算法,此算法重点关注并行训练。
在$A3C$中,由critics 学习价值函数,多个actors进行并行训练并且不断和全局参数进行同步。可以看出A3C是专门针对并行训练设计的。
以使用状态价值函数为例,如果我们使用MSE (均方误差)为loss函数:$J_v(w) = (G_t - V_w(s))^2$,那么我们可以使用梯度下降算法来找到最优参数$w$。这个状态价值函数也被用作策略梯度更新时的基线值。
算法基本步骤如下:
- 设定全参数$\theta, w$,以及特定线程的参数$\theta^\prime, w^\prime$
- 初始化时间步数$t=1$
- 当$T \le T_{MAX}$:
- 重置梯度值:$d\theta = 0, dw=0$
- 线程相关参数使用全局参数进行同步:$\theta^\prime = \theta, w^\prime = w$
- 令$t_{start} = t$,并且对初始状态进行采样$s_t$
- 当$s_t$不是终止态并且$t - t_{start} \le t_{max}$:
- 选择一个行为$A_t \sim \pi_{\theta^\prime} (A_t|S_t)$,执行$A_t$得到新的奖励$R_t$和下一个状态$s_{t+1}$
- 更新$t = t+1, T=T+1$
- 计算最后状态的收益估计:
- $R=0$,如果$s_t$为终止态
- $R=V_{w^\prime} (s_t)$,如果$s_t$为非终止态
- For$i = t-1,\ldots, t_{start}$:
- $R \leftarrow \gamma R + R_i$
- 计算$\theta^\prime$累计梯度:$d\theta \leftarrow d\theta +\nabla_{\theta'} \log \pi_{\theta'}(a_i\vert s_i)(R - V_{w'}(s_i))$
- 计算$w^\prime$累计梯度:$dw \leftarrow dw + 2 (R - V_{w'}(s_i)) \nabla_{w'} (R - V_{w'}(s_i))$
- 使用累计梯度$d\theta, d w$更新参数$\theta, w$
使用A3C可以使用多个执行代理(agent)来进行并行训练。梯度的累积可以看做是随机梯度更新算法中多个$minibatch$的聚合;$\theta, w$的值每次会被不同的训练线程独立地进行微小的更新。
A2C
A2C是$A3C$的同步、确定性版本。这也是它为什么被命名为$A2C$的原因,它将$A3C$中的第一个A (asynchronous) 省略了。在A3C中,每一个执行代理与全局参数独立地进行参数同步,这会导致在某同一时刻,不同的执行代理训练所用的参数的版本不一致,因此聚合后的参数可能不是最优的。为了解决这种不一致性,在A2C中,每一轮都会等待所有执行代理执行完毕后再进行梯度的聚合。这样下一轮开始时,所有的执行代理都会使用同样最新参数的策略。同步梯度更新方法让训练过程更加专注,并且一定程度上可以让加快收敛速度。
在openai的实验结果中,A2C表现出了更高GPU利用率;在使用大的batch size的时候,A2C可以工作的更好,并且可以取得与A3C同样甚至更优的性能表现。
下图展示了A3C和A2C基本结构差异的一个对比:
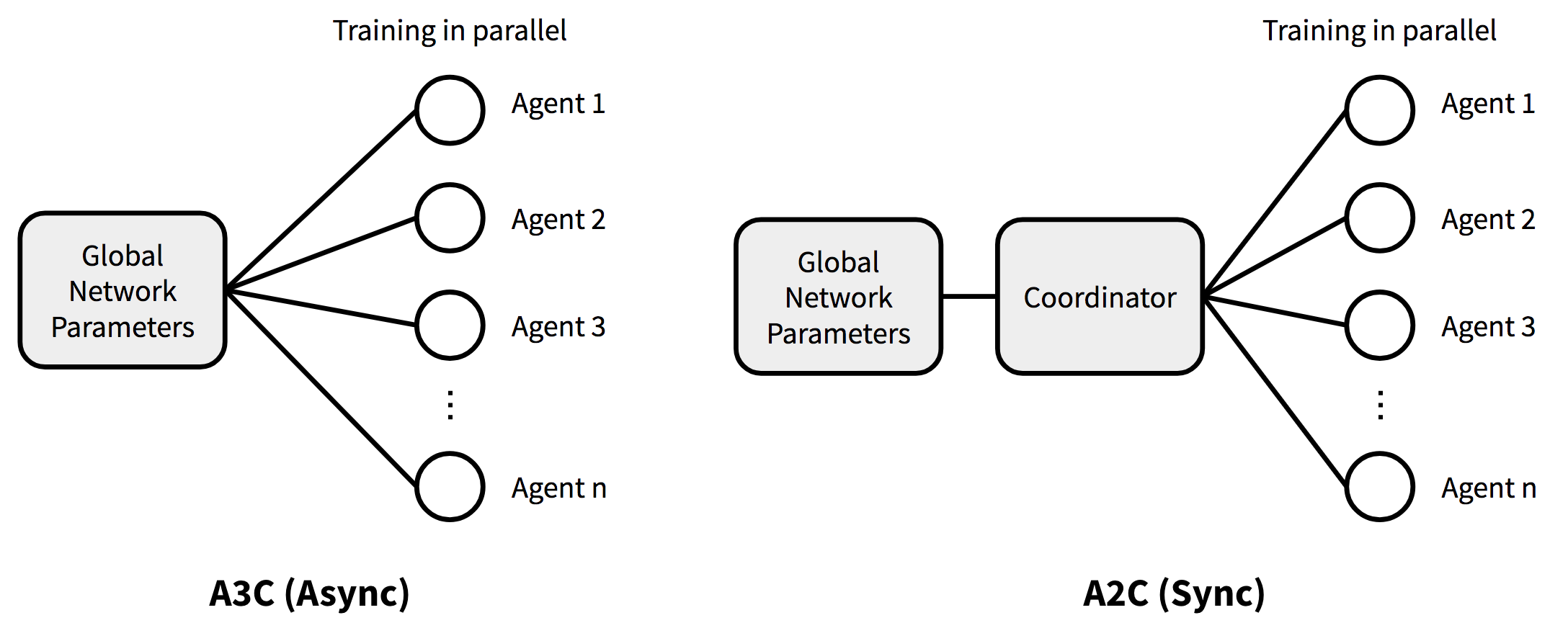
DPG
[论文]
在我们上述提到的方法中,所有的策略函数$\pi(\cdot|s)$都被建模为一个在行为空间$\mathcal{A}$上的一个概率分布,因此这里的策略都是随机策略。在DPG(deterministic policy gradient),也就是确定性策略梯度中,策略被建模为仅会输出一个确定性行为:$a=\mu(s)$。这看起来很奇怪,策略如果输出单个确定的行为,那么行为概率的梯度如何计算呢?下面我们一步步来看。
首先我们定义一些新的符号来帮助理解和讨论:
- $\rho_0(s)$: 状态初始分布
- $\rho^\mu(s \to s', k)$: 从状态s开始,根据策略$\mu$来执行$k$步之后到达状态$s^\prime$的概率密度函数
- $\rho^\mu (s^\prime)$: 带衰减系数的状态分布,定义为:$\rho^\mu(s') = \int_\mathcal{S} \sum_{k=1}^\infty \gamma^{k-1} \rho_0(s) \rho^\mu(s \to s', k) ds$
优化的目标函数为:
确定性策略梯度定理:现在是时候计算梯度了!根据链式法则,我们首先计算$Q$对$a$的梯度,然后计算确定性策略$\mu$对$\theta$的梯度:
我们可以将确定性策略看作是随机策略的一种特殊形式,也就是策略的概率分布仅在某一个行为$a$上有非零概率。实际上,在DPG的论文中,作者指出:如果对随机策略$\pi_{\mu_{\theta},\sigma}$,通过确定性策略$\mu_\theta$和一个随机变量$\sigma$进行重参数化(re-parameterize),那么随机策略最终会在$\sigma=0$时与确定性策略等价。由于随机策略需要对整个状态和动作空间进行积分,我们可以预计它需要比确定性策略更多的样本。
确定性策略定理可以被应用到一般策略梯度算法的框架中。
我们以一个on-policy的actor-critic算法为例展示DPG的工作过程。在on-policy的actor-critic算法每一次迭代的过程中,策略输出的行为都是确定的,策略参数的更新方法如下:
由于DPG的策略所输出的行为都是确定的,在没有引入足够随机性的情况下,很难保证采样过程会进行足够的探索(exploration)。因此,要么我们在策略中引入随机噪声(实际上,这样确定性策略就变成不确定了);要么我们可以使用off-policy方法通过使用一个不同的随机行为策略生成训练样本来进行训练。
假设在off-policy方法中,训练样本路径是通过一个随机策略$\beta(a|s)$生成的,此时状态分布遵从相应的带衰减的状态概率密度$\rho^\beta$:
注意,由于策略是确定的,我们仅需要使用$Q^{\mu} (s, \mu_0(s))$而不是$\sum_a \pi(a \vert s) Q^\pi(s, a)$来作为状态$s$的奖励估计。在使用随机策略的off-policy方法中,重要性采样(importance sampling)经常被用于修正行为策略与目标策略不一致所带来的误差。而在确定性策略梯度算法中,我们无需对行为进行积分,因此我们无需进行重要性采样。
DDPG
DDPG(Lillicrap, et al., 2015)(Deep Deterministic Policy Gradient)是一个model-free、off-policy的actor-critic算法,它将DPG算法和DQN算法结合了起来。我们回顾一下,DQN(Deep Q-Network)通过经验回放(experience-replay)以及目标网络冻结来稳定$Q$函数的学习过程。原始的DQN工作在离散空间中,DDPG结合了actor-critic框架,将DQN扩展到连续空间上,并且用其学习一个确定性的策略。
为了更好的进行探索,我们通过给确定性策略$\mu_\theta (s)$添加噪声$\mathcal{N}$来得到一个新的探索策略$\mu^\prime$:
此外,DDPG对于actor和critic参数的更新都是软更新("保守的策略迭代")。软更新不会直接使用新策略的参数,而是将新旧策略进行加权求和,也就是在参数更新时,引入了一个参数$\tau \ll 1$,并使用该参数进行更新操作:$\theta' \leftarrow \tau \theta + (1 - \tau) \theta'$。使用此方法,可以限制目标网络的更新速度。这与DQN中的设计不一样,在DQN中目标网络会在一定的时间段内被冻结。
文中提到的一个细节在机器人技术中特别有用,它是关于如何对低纬度特征的不同的物理单元进行归一化的问题。举例来说:我们设计了一个模型,它以机器人的位置以及速度作为输入,并以此来学习某个策略;这些物理量在本质上是不同的,同种类型的数据对于不同的机器人来说变化量可能非常大。文中就引入了Batch normalization来解决此类问题。算法截图图下:

D4PG
[论文]
D4PG (Distributed Distributional DDPG)在DDPG的基础上进行了一系列的改进,来让DDPG可以以分布式的方式运行。改进点有:
(1)分布式Critic: critic 用于对Q的期望值进行估计,Q值被看作一个服从分布$Z_w$的一个随机变量,因此$Q_w(s, a) = \mathbb{E} Z_w(x, a)$。优化目标是最小化两个分布之间的距离—分布式TD误差:$L(w) = \mathbb{E}[d(\mathcal{T}_{\mu_\theta}, Z_{w'}(s, a), Z_w(s, a)]$,其中$\mathcal{T}_{\mu_\theta}$为贝尔曼操作子。
确定性策略梯度更新公式变为:
(2)N步回报: 在计算TD误差时,D4PG计算了N步的TD值,而不是单步,新的TD目标值为:
(3)多个分布式并行actors: D4PG利用K个独立的actors来并行采集样本,并将其存储到一个统一的重放缓冲区中。
(4)带优先级的经验回放 (Prioritized Experience Replay, PER): 修改的最后一部分是关于如何从重放缓冲区中进行采样的。PER并非使用均匀分布进行采样,不同的样本被采样的概率不一样。假设重放缓冲区大小为$R$,样本$i$的采样概率为$(Rp_i)^{-1}$,也就是样本的重要性权值为$(Rp_i)^{-1}$。
下面的论文截图展示了D4PG算法,论文中的一些变量表示方法与本文中使用的有一些差别;比如我们使用$\mu(\cdot)$来表示确定性策略而不是$\pi(\cdot)$。

MADDPG
多执行体DDPG (Multi-Agent DDPG, MADDPG)扩展了DDPG算法,以使其可以工作在一个新的环境中。在此环境中,多个执行体需要合作来完成某项任务,但是这些执行体仅能观测到执行体本地信息。在单个执行体的观察中,它看到的环境是非平稳的,这种非平稳性是由各个执行体策略不断更新而这些更新又不是全局可知所造成的。MADDPG是一个actor-critic模型,它被特别设计用于处理这种可以与多个执行体进行交互的、策略不断变化的环境。
前面提到的问题可以在MDP的多执行体(multi-agent)版本中进行形式化描述,它们通常被称为马尔可夫博弈(Markov games)。MADDPG就是针对部分可观察马尔可夫博弈问题提出的。假设我们一共有N个执行体,并且有一个状态集合$\mathcal{S}$。每个执行体$1, 2, ..., N$拥有各自行为的集合$\mathcal{A}_1, \dots, \mathcal{A}_N$,以及各自的观测状态集合$\mathcal{O}_1, \dots, \mathcal{O}_N$。定义状态转移函数包含所有执行体的状态、行为以及观测值空间:$\mathcal{T}: \mathcal{S} \times \mathcal{A}_1 \times \dots \mathcal{A}_N \mapsto \mathcal{S}$。对于每一个执行体,它的策略仅会作用于它自己的观测空间上。如果策略是随机的,将其表示为:$\pi_{\theta_i}: \mathcal{O}_i \times \mathcal{A}_i \mapsto [0, 1]$;如果策略是确定性的,将其表示为:$\mu_{\theta_i}: \mathcal{O}_i \mapsto \mathcal{A}_i$。
我们使用符号$\vec{o}, \vec{\mu}, \vec{\theta}$分别表示:$\vec{o} = {o_1, \dots, o_N}, \vec{\mu} = {\mu_1, \dots, \mu_N}, \vec{\theta} = {\theta_1, \dots, \theta_N}$。
MADDPG中的critic是一个中心化的critic,这里的中心化指的是critic可以使用所有执行体的相关数据(比如:执行的动作、观测到的状态等)。每个执行体会学习一个自己的行为价值函数$Q^\vec{\mu}_i(\vec{o}, a_1, \dots, a_N)$,可以看到这里的$Q$的输入使用到了所有其它执行体相关的数据,其中$a_1 \in \mathcal{A}_1, \dots, a_N \in \mathcal{A}_N$是$N$个执行体所执行的动作。每个执行体的$Q_i^{\vec{\mu}}$函数都是独立进行训练学习的,它们奖励(rewards)的结构可能会出现任意的结构,包括它们可能会去竞争奖励。
每个执行体$i$也拥有一个actor,用于进行策略探索以及策略参数$\theta_i$的更新。
Actor 的更新:
其中$D$是经验回放的存储缓冲,其中包含了许多轮所收集到的样本:$(\vec{o}, a_1, \dots, a_N, r_1, \dots, r_N, \vec{o}')$,该样本表示从当前的观测状态$\vec{o}$开始,每个执行体分别执行动作$a_1, \ldots, a_N$,并且获取得到了奖励$r_1, \ldots, r_N$, 最终进入到下一个状态$\vec{o}^\prime$。
Critic 的更新:
其中$\vec{\mu}^{\prime}$为确定性的目标策略,它使用软更新进行参数的更新。
如果在critic更新的时候,策略$\vec{\mu}^\prime$还是未知的,我们可以让每一个执行体学习、演化出其它执行体策略的近似策略。使用这些近似策略,MADDPG仍然可以有效地进行训练学习(虽然可能不太精确)。
为了缓解不同执行体之间的竞争或者合作带来的高方差,MADDPG提出了引入一个新方法-策略集成 (policy ensembles):
- 每个执行体训练K个策略
- 每一轮随机选择一个策略公开
- 使用K个策略集成的结果进行策略更新
总结一下,MADDPG在DDPG基础上添加了三个额外的部分来让算法可以被应用到多执行体环境中:
- 中心化的critic + 分布式的actor
- 某个执行体的actor需要有估计其它执行体策略的能力
- 使用策略集成来降低方差
下图为论文中MADDPG架构示意图:
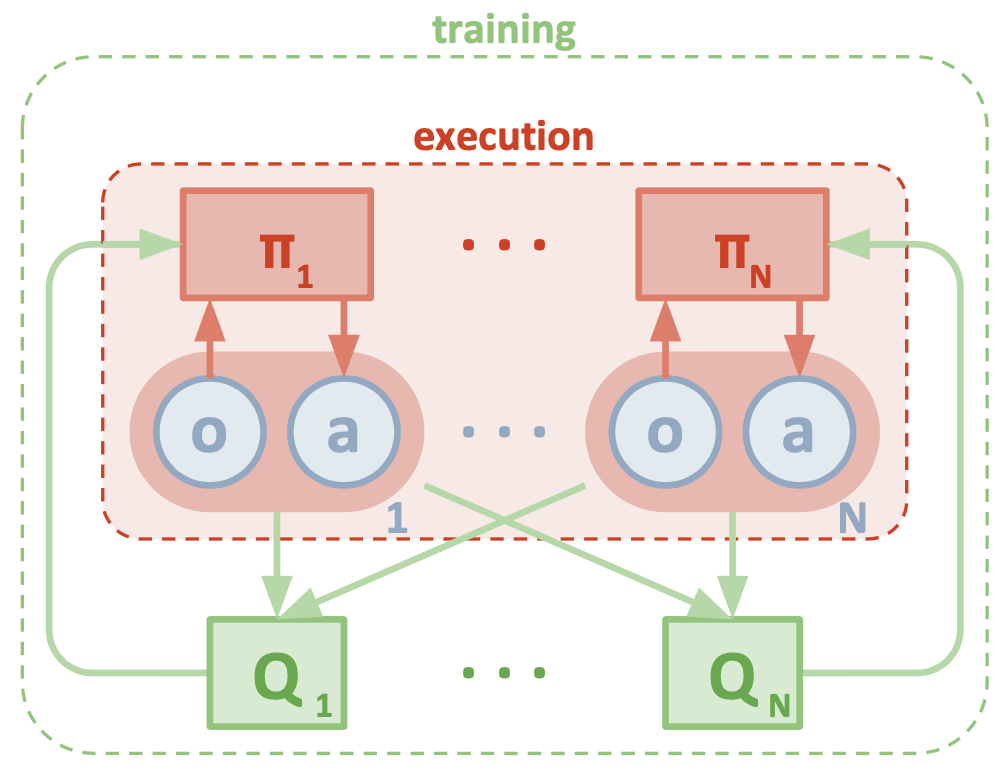
TRPO
为了改进训练的稳定性,我们应该避免在单次更新时策略参数改动太大。TRPO (Trust region policy optimization)通过在每次迭代时对策略更新的大小使用KL散度来进行约束以实现这一想法。
考虑这样一个情形,当我们执行off-policy RL算法时,我们用于收集样本路径的策略$\beta$与我们所优化的目标策略是不一样的。Off-policy模型中的目标函数会对所采集样本的优势值(A = Q-V)进行计算求和,而目标策略的分布与我们生成样本所用的行为策略的分布是不一致的(存在差异,会定期同步)。为了解决这种不一致性带来的误差,TRPO会使用我们之前提到的重要性权重$\cfrac{\pi_\theta(a|s)}{\beta(a|s)}$对此误差进行修正。这样我们可以得到目标函数:
其中$\theta_{old}$是梯度更新前的参数,其它符号含义与前文一致。注意这里我们使用了优势函数的估计$\hat{A}_{\theta_{old}}$而不是优势函数本身,优势函数本身$A(\cdot)$是未知的。
在进行on-policy训练时,理论上说我们用于收集样本的策略与我们想要优化的目标策略是一样的。但是,在一个异步并行训练的环境下,我们采集样本所用的行为策略可能与我们的目标优化策略产生差异。TRPO考虑到了这个微小的差异:它将行为策略标记为$\pi_{\theta_\text{old}}(a \vert s)$,这样优化的目标函数就变为:
为了保证新旧策略间的差异不会太大,TRPO使用KL散度来限制新旧策略分布之间的距离。因此目标函数$J(\theta)$优化时,需要满足如下限制:
其中$\delta$为超参,用于限制两个分布之间的距离,$D_{KL}$为KL散度的算子。在满足这个限制的条件下,TRPO可以在策略迭代的过程中,保证改进方向的单调性(持续改进,不会变坏)。
PPO
我们看到TRPO算法较为复杂,还需要进行KL散度的计算,本小节所介绍的PPO算法使用了一个简单的方法对TRPO进行了改进。PPO (Proximal Policy Optimization)中使用了一个简洁的、截断式的目标函数来达到与TRPO相似的性能表现。
首先,我们定义新旧策略比为:
这样,TRPO (on-policy)的目标函数变为:
如果不对$\theta_{old}$与$\theta$之间的距离进行限制,对于$J^{TRPO}(\theta)$的优化很可能会导致参数的更新值非常大,进而导致训练极其不稳定。PPO中通过将比例$r(\theta)$的大小强制限制在1左右(准确来说限制在$[1-\epsilon, 1+\epsilon]$之间,$\epsilon$为一个超参数),来限制策略参数的变化量。那么截断式的优化目标函数为:
上式中 clip 函数,让比例$r(\theta)$不会大于$1+\epsilon$,不会小于$1-\epsilon$。PPO的目标函数会选择原始目标函数与clip之后的目标函数中的较小版本。这样优化器就不会盲目让参数往可以让当前样本的奖励变得非常大的方向去移动。
如果在使用PPO的时候,所设计的策略模型(actor)与价值模型(critic)共享了部分参数,那么除了使用上面的截断式目标函数之外,目标函数还可以添加价值函数的惩罚项和一个熵(entropy)的惩罚项:
其中,红色部分为价值函数的惩罚项,蓝色部分为熵惩罚项,$c_1, c_2$是用于调节的超参数。添加熵惩罚项的目的是保证足够的探索(exploration)。
PPO算法在许多基线任务上都进行过测试,被证明简洁高效。
在后续的论文[Hsu等人, 2020]中,PPO中的两个设计选择被重新审视了,也就是:(1) 用于策略正则化的截断式的比例$r(\theta)$和 (2) 使用连续高斯或者离散softmax分布对策略行为空间进行采样。该论文首先列出了PPO算法的三个失败的情况:
- 在连续的行为空间下,标准的PPO算法在奖励超出所能支持的边界之后,会变得不稳定
- 在离散的行为空间下,如果奖励非常稀疏并且在某些行为上的奖励非常高的时候,标准PPO算法会停留在局部最优的行为上
- 在初始化数据接近局部最优解时,策略对于初始化非常敏感
文中提出了两个替换的设计方案来解决上述问题:
- 为了解决高斯策略相关的问题1&3,文中提出将行为空间离散化或者使用Beta分布来帮助避免这些问题
- 针对问题1&2,文中提出使用KL正则(和TRPO中一样)来作为替代模型
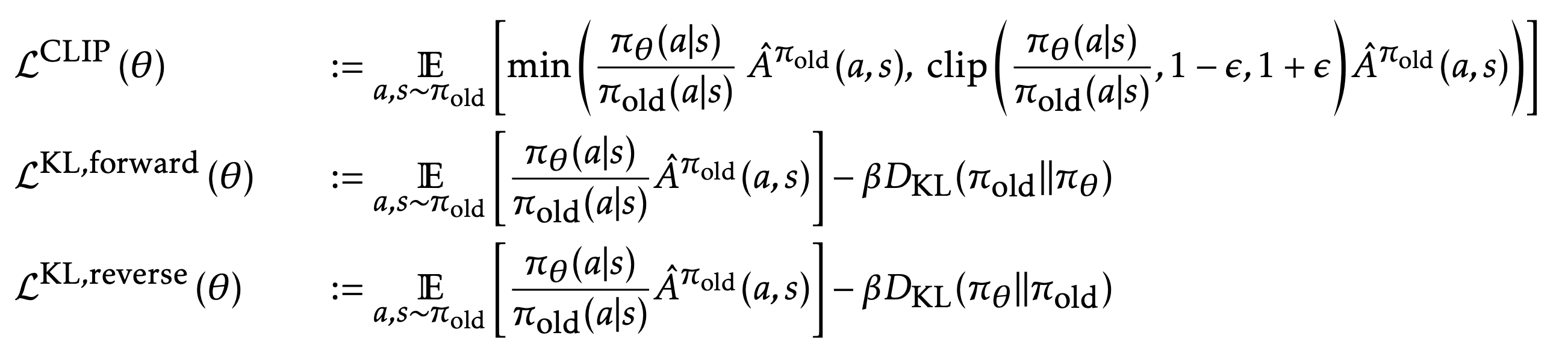
PPG
让策略网络与价值网络间共享参数(共享神经网络层)是一把双刃剑。这种方法虽然可以让策略网络与价值网络来共享学习到的特征,但是引起两个模型之间的竞争冲突。策略网络与价值网络对于同一参数的优化方向是不一致的。PPG (Phasic Policy Gradient)对于传统的on-policy的actor-critic算法(PPO)进行了修改,以使其可以将策略网络的训练与价值网络的训练分在不同的阶段中进行:
- 策略阶段:使用PPO的目标函数$L^\text{CLIP} (\theta)$来优化策略网络
- 辅助阶段:优化辅助目标函数。在论文中,值函数的误差是唯一的辅助目标,但是辅助目标函数也可以添加一些其它项
除了PPO中的$L^{CLIP}(\theta)$之外,文中还定义了两个目标函数:联合目标函数和辅助目标函数,公式如下:
其中$\beta_{clone}$是一个超参数用于控制在辅助阶段允许策略更新的程度。算法如下:

其中:
- $N_\pi$为在策略阶段策略更新迭代的次数。
- $E_\pi$和$E_V$控制了样本重用的迭代次数(一个用于策略函数,一个用于价值函数),这两个参数都是用于策略阶段的
- $E_{aux}$定义了在辅助阶段样本重用的次数;论文的实验使用的参数为:$E_{aux}=6, E_{\pi}=E_V=1$
PPG在采样效率上相对于PPO来说有很大改进,下图是PPG和PPO性能表现归一化之后的对比图,PPG看起来好多了。
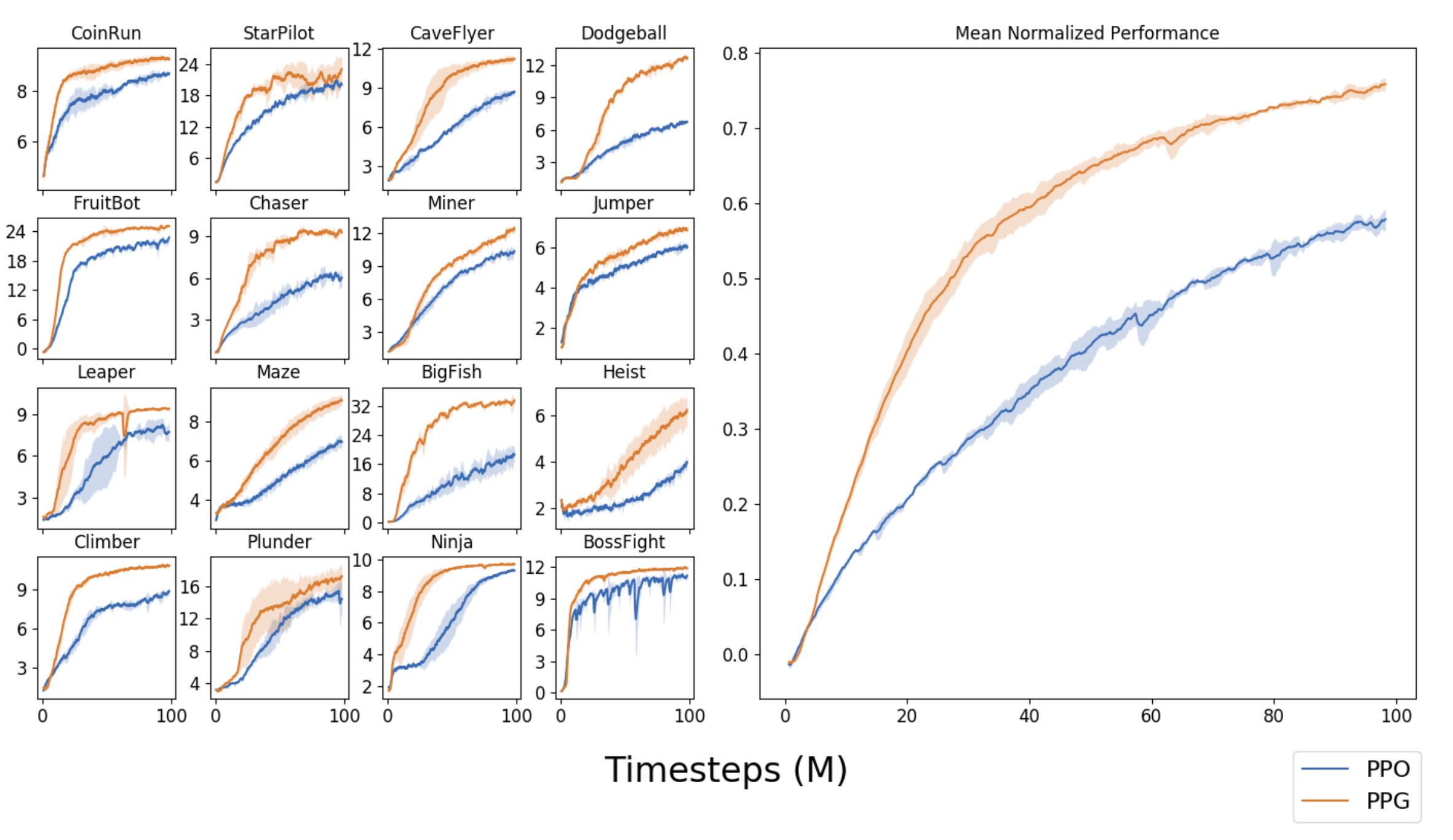
ACER
ACER (Actor-Critic with Experience Replay), 是一个off-policy的actor-critic 模型,当然它也会使用经验重放来提高样本效率,降低数据相关性。A3C构成了ACER算法的基础,但A3C是on-policy的。ACER是A3C的一个off-policy的版本。让A3C由on-policy变为off-policy的一个主要障碍就是如何控制off-policy预测器的稳定性。ACER提出了三个设计来解决这个问题:
- 使用Retrace Q值估计
- 使用带偏差修正的截断式重要性权重
- 应用高效TRPO
Retrace Q值估计
Retrace是一个off-policy的Q值估计算法,它依赖于环境收益,对于目标策略以及行为策略$(\pi, \beta)$的收敛性都有很好的保证,并且数据使用效率也不错。
我们回顾一下TD学习是如何用于预测的:
- 计算TD误差:$\delta_t = R_t + \gamma \mathbb{E}_{a \sim \pi} Q(S_{t+1}, a) - Q(S_t, A_t)$;$r_t + \gamma \mathbb{E}_{a \sim \pi} Q(s_{t+1}, a)$就是大家所熟知的TD目标(TD target)值。式中我们使用了期望符号$\mathbb{E}_{a \sim \pi}$,这是因为对于未来收益我们能做的最好估计就是服从当前的策略$\pi$
- 通过将价值函数往目标值移动来更新$Q$值:$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \delta_t$。可以看到$Q$值的改变量与TD误差成正比:$\Delta Q(S_t, A_t) = \alpha \delta_t$。
这个过程是off-policy的,我们需要对$Q$值的更新使用重要性采样:
重要性权重的乘积看起来非常可怕,因为它可能会引入巨大的方差。RetraceQ值估计方法对$\Delta Q$进行了修改,对于重要性权重进行了截断:
ACER 使用$Q^{ret}$作为训练的目标值,并且使用L2 loss函数:$(Q^\text{ret}(s, a) - Q(s, a))^2$。
重要性权重截断
为了降低策略梯度$\hat{g}$的高方差,ACER对于重要性权重使用常量$c$进行了截断,并且在后面添加了一个修正项。符号$\hat{g}_t^{acer}$是时刻$t$时ACER的策略梯度。
其中$Q_w(\cdot), V_w(\cdot)$是critic估计的价值函数。上式中的第一项(蓝色部分)包含了截断后的重要性权重。在使用$V_w(\cdot)$作为基线值的基础上,截断操作可以进一步帮助降低方差。第二项(红色部分)对于前面一项的截断进行了修正以获得一个无偏估计。
高效TRPO
进一步地,ACER采纳了TRPO的思想,但是做了一点小小的改进来让计算更加地高效:ACER在每次迭代过程中不再去计算新旧策略分布之间的KL散度,取而代之的是,ACER维持了一个以往策略的滑动平均值以保证更新后的策略不致于偏离之前的平均策略太远。
ACER论文中使用了大量的公式对读者的大脑进行了轰炸。但是在拥有TD-learning, Q-learning,重要性采样,以及TRPO的知识之后,你可能会发现它会变得稍微容易理解一点。
ACTKR
ACKTR (Actor-Critic using Kronecker-factored Trust Region)提出使用二阶优化算法K-FAC (Kronecker-factored Approximation Curvature)来更新cirtic和actor的参数。K-FAC对于自然梯度的计算进行了改进。自然梯度与我们常使用的标准梯度下降有很大不同,这里有一个很直观的解释,下面使用一句话概括:
"假设我们的网络定义在一个参数空间里,那么我们考虑那些与我们旧的网络之间的距离为一个常量的所有参数的集合(这个常量可以看做是step size或者学习率),在这个参数的集合中,我们挑选一个可以让我们的loss函数最小的那一个。"
我将ACKTR算法列在这里主要是考虑到这篇文章的完整性,这里不会太深入到该算法的细节中去。因为它需要很多自然梯度的知识及其相关的优化算法。如果感兴趣,可以查看论文或者一些博文,阅读ACKTR论文之前,请先看下表列出的内容:
- Amari.Natural Gradient Works Efficiently in Learning. 1998
- Kakade.A Natural Policy Gradient. 2002
- A intuitive explanation of natural gradient descent
- Wiki: Kronecker product
- Martens & Grosse.Optimizing neural networks with kronecker-factored approximate curvature. 2015
这里给出一个K-FAC论文的一个顶层视图总结:
"近似方法分为两阶段。
在第一阶段,Fisher矩阵的行和列被分成不同的组,每一个对应一层中的所有权重值,这实际上进行了一次矩阵迭代分块操作。这些块之后会使用小矩阵的Kronecker积来近似。这个操作等效于对网络梯度的统计数据进行一些特定的近似猜想。
在第二阶段,该矩阵被进一步近似为拥有一个具有逆矩阵的块对角或者块对三角矩阵。我们仔细检查了逆协方差、树形结构的图模型和线性回归之间的关系之后,发现这种近似是合理的。需要注意的是,这种验证对于Fisher矩阵本身并不适用。我们的实验证实,虽然Fisher矩阵的逆确实(近似)具有这种结构,但是Fisher矩阵本身并没有。"
SAC
SAC (Soft Actor-Critic)将策略的熵纳入训练的最终目标考量,用于鼓励探索,算法期望在保持策略尽可能随机的情况下,仍然可以成功完成某项任务。SAC是一个基于最大熵RL的一个off-policy + actor-critic的模型。
SAC由三个重要部分组成:
- 由独立的策略网络和价值网络组成的actor-critic结构
- 一个off-policy的训练方式,可以提高数据有效性
- 引入最大熵来确保稳定性和探索
策略的训练目标是同时最大化期望收益和熵值:
其中$\mathcal{H}(.)$为熵度量,$\alpha$为控制系数(也叫做温度(temprature))。让熵值最大化可以使策略:(1) 进行更多的探索,(2) 抓住更多近似最优的策略 (就是说,如果存在多个同样好的策略,它们应该可以以相同的概率被选择)。
准确来说,SAC目标在于学习三个函数:
- 策略$\pi_\theta$,参数为$\theta$
- 由参数$w$决定的(Soft)Q价值函数
- 由参数$\psi$决定的(Soft)状态价值函数$V_\psi$;理论上,如果我们已知$Q$和$\pi$,我们可以推导出$V$,但是实际运行时,独立的$V$可以让训练更加稳定
Soft Q函数和Soft状态价值函数定义为:
$\rho_\pi(s)$和$\rho_\pi(s, a)$与我们上文DPG章节中定义类似,为遵循策略$\pi$的边缘分布。
状态价值函数的loss函使用MSE loss,loss函数及其梯度为:
$D$为样本重放缓冲区。
Soft Q函数的训练目标是最小化soft贝尔曼残差, loss及其梯度为:
其中$V_{\bar{\psi}}$也是状态价值函数,只不过它是$V_{\psi}$的一个指数滑动平均(或者使用类似DQN中Q网络那种定期更新的方式进行更新),这种更新方式可以让训练更加稳定。
SAC策略更新的目标是最小化KL散度:
其中$\Pi$为一个潜在策略的集合,这些潜在策略服从一些我们已知的、方便处理的一些分布。比如说:$\Pi$可以是高斯混合分布家族,这种分布虽然建模困难,但是表达性强也能处理。$Z^{\pi_\text{old}}(s_t)$是对分布进行归一化的配分函数,通常我们无法处理它,但是它对梯度没影响。如何最小化$J_\pi(\theta)$取决于我们对$\Pi$的选择。
上述的更新规则可以保证$Q^{\pi_\text{new}}(s_t, a_t) \geq Q^{\pi_\text{old}}(s_t, a_t)$,此引理的证明可以看到原始论文的附录B.2。
有了上述目标函数及其梯度之后,算法看起来就直观了:

带温度动态调整的SAC
SAC算法对于温度参数非常敏感,不幸的是调整温度参数是很困难的。这是因为在训练过程中随着策略不断被优化,熵变得难以预测,而且对于不同的任务,策略熵值也是不一样的。对于SAC的改进促成了一种新的条件优化问题的出现:在最大化期望收益的同时,策略应该满足最小熵限制:
其中$\mathcal{H}_0$是估计的最小熵阈值。
期望收益$\mathbb{E} \Big[ \sum_{t=0}^T r(s_t, a_t)\Big]$可以分解为所有时刻奖励的总和。由于时刻$t$时的策略$\pi_t$对于前一时刻$t-1$的策略$\pi_{t-1}$无影响,我们可以按照时间顺序从后向前来优化收益:
这里我们设$\gamma=1$。
我们从最后的时刻$T$开始优化:
首先,我们定义如下函数:
带入优化公式有:
为了解决这个带不等式约束的优化问题,我们可以用拉格朗日算子$\alpha_T$(对偶变量)构建拉格朗日表达式:
考虑如下问题:给定一个特定值$\pi_T$以及$\alpha$,我们希望最小化$L(\pi_T, \alpha_T)$:
- 如果约束满足,也就是$h(\pi_T) \ge 0$,那么显然最优的情况是,我们设置$\alpha=0$,因此$L(\pi_T, 0) = f(\pi_T)$
- 如果约束不满足,也就是$h(\pi_T)\lt 0$,那么我们可以设置$\alpha_t\to\infty$,此时我们有$L(\pi_T, \infty) = -\infty = f(\pi_T)$
这两种情况下,我们都有:
这样,我们可以得到约束优化的对偶问题:
我们可以对$\pi_t$和$\alpha_T$进行迭代优化。首先我们可以固定$\alpha_T$,此时去优化$\pi_T$来最大化$L(\pi_T^*, \alpha_T)$;而后,我们固定策略$\pi_T$,去优化$\alpha_T$来最小化$L(\pi_T^{*}, \alpha_T)$。假设我们有两个神经网络分别用于策略网络和温度参数,迭代训练的过程和我们平常优化网络的方法一致:
因此,我们有:
现在我们回头看Soft Q价值函数:
由此可以得到时刻$T-1$的最优回报:
和前面的步骤类似:
上式中绿色部分用于更新$\alpha_{T-1}$,形式上和前文蓝色部分更新$\alpha_{T-1}$的公式形式上是一样的。通过不断重复这个过程,我们可以在每一步中优化下面的目标函数,来获取最优的温度参数:
最终,算法除了通过目标函数$J(\alpha)$来学习$\alpha$值完,流程基本和SAC一样:

TD3
大家知道Q-learning算法的价值函数有超估(overestimation)的问题。这个超估问题会随着训练的迭代传播,最终会对策略产生负面影响。这也是Double Q-learning和Double DQN被提出的原因:行为选择和$Q$值更新使用了两个不同的网络来解偶。
TD3 (Twin Delayed Deep Deterministic)算法在DDPG的基础上应用了一些列的小技巧来防止值函数的超估问题:
(1)截断式Double Q-learning: Double Q-learning中行为选择和$Q$值预测使用了两个分离的网路。在DDPG中,给定两个确定性的actors$(\mu_{\theta_{0}}, \mu_{\theta_{1}})$以及两个相应的critics$(Q_{w_1}, Q_{w_2})$,Double Q-learning的贝尔曼方程如下:
但是由于策略更新缓慢,这两个网络太相似了,以至于它们无法做出相互独立决定。截断式Double Q-learning使用两个预测中较小的那个值,这个做法让算法更加偏向欠估计(underestimate)的偏差,而这个在训练中很难传播:
(2)目标和策略网络延迟更新:在actor-critic 模型中,策略和价值网络的更新紧密联系在一起:当策略网络的估计不准确的时候,价值网络会因为超估问题导致无法收敛;而如果价值网络估计不准确又会导致策略网络变得更差。
为了降低方差,TD3相比于Q函数来说以一个更低的频率去更新策略。策略网络在价值网络的误差尚未足够小时,保持不变。TD3为价值函数引入了一个平滑的正则策略:在每个mini-batch熵,给选定的行为(action)添加少量的截断式的随机噪声:
这个方法和SARSA更新的思想类似,可以强制让相似的动作可以有相似的价值。最终算法如下:

SVPG
SVPG (Stein Variational Policy Gradient)应用SVGD算法来优化策略参数$\theta$。在策略熵最大化优化的开始,$\theta$被看作是一个随机变量$\theta\sim q(\theta)$,而模型用来学习分布$q(\theta)$。如果我们有先验知识,知道分布$q$是什么样的,比如可能与分布$q_0$类似,那么我们希望在训练过程中可以让$q(\theta)$不要与$q_0$相差太大。因此,设计如下目标函数:
其中,$\mathbb{E}_{\theta \sim q} [J(\theta)]$为$\theta\sim q(\theta)$条件下的期望收益,$D_{KL}$为$KL$散度。
如果我们没有任何先验信息,我们可以设置$q_0$为均匀分布,并且设置$q_0(\theta)$为一个常量。这样上面的目标函数就变成了SAC,其中熵那一项用于加强探索:
我们对目标函数对$q$进行进行求导,有:
最优分布为:
温度系数用于在利用(exploitation)和探索(exploration)*之间进行平衡。当$\alpha\to0$,$\theta$的更新仅与期望收益$J(\theta)$有关。当$\alpha\to\infty$,$\theta$仅关注先验分布。
用SVGD方法预测目标函数的后验概率$q(\theta)$时,它依赖于许多点(particle)$\{ \theta_i \}_i^n$(独立训练的策略代理),每一个的更新规则为:
上式中,$e$为学习率,$\phi^{*}$是$\theta$向量的一个RKHS$\mathcal{H}$(再生希尔伯特空间)中的单位球,$q'$为分布$\theta+\epsilon \phi(\theta)$。
比较不同基于梯度的更新方法:
| 方法 | 更新($\Delta\theta$)空间 |
|---|---|
| 朴素梯度 | 参数空间 |
| 自然梯度 | 搜索分布空间 |
| SVGD | 核函数空间 |
$\phi^{*}$的一个估计有如下形式,可以使用一个正定核$k(\vartheta, \theta)$,比如高斯RBF核来测量不同点(particle)间的相似度:
上述公式中:
- 左边红色部分鼓励参数往$q$概率大的方向移动(该方向由相似的点共享)。=> 为了与其它点相似
- 右边绿色部分将一个点$\theta$往远离其它点的方向移动,以让策略更加多样化。=>为了让不同点之间差异变大
通常,我们会让温度调节遵循一个类似退火的方案,这样训练会在开始时多去探索,而在快要结束时更多进行利用(exploitation)。
算法截图如下:

IMPALA
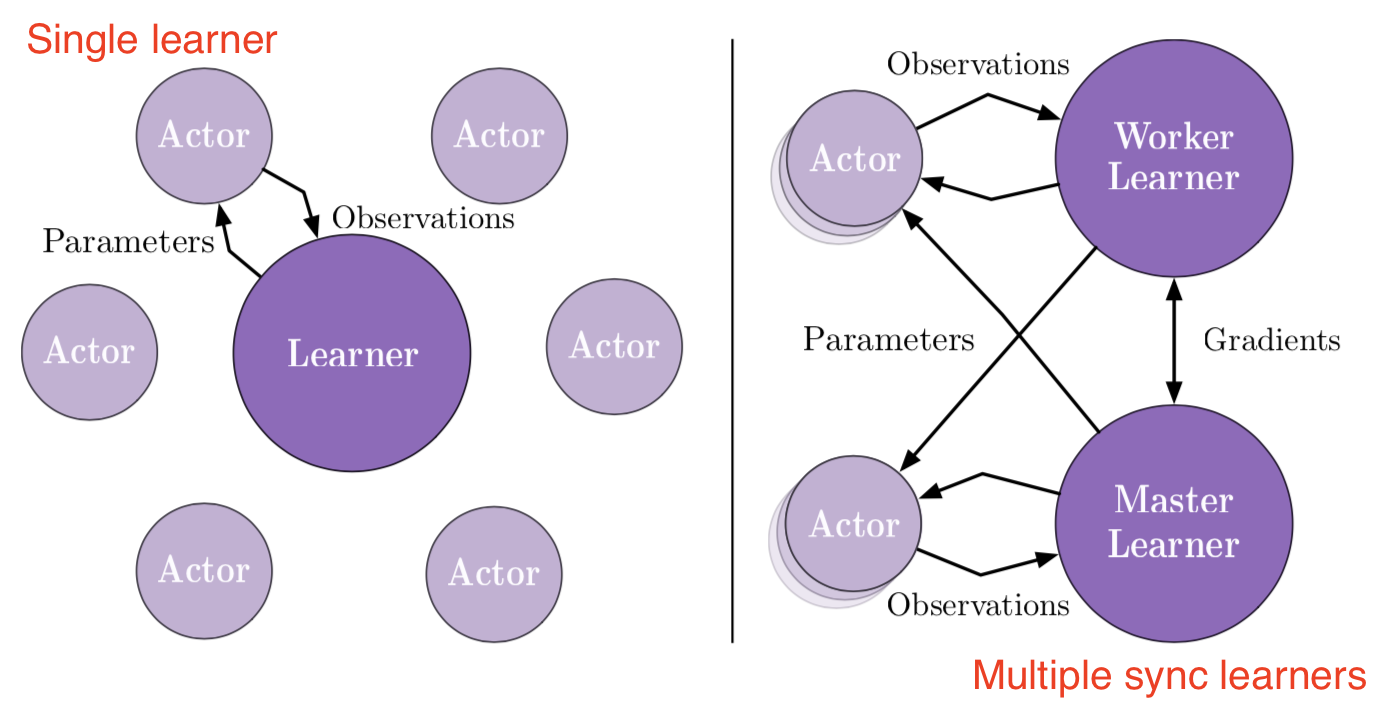
为了让RL的训练可以达到一个非常高的吞吐量,IMPALA (Importance Weighted Actor-Learning Architecture)框架在基本的actor-critic基础上将动作执行(acting)与学习(learning)过程分离,使用V-trace off-policy修正进行经验路径(experience trajectories)进行学习。
多个actors并行生成经验数据,学习器使用所有生成的数据去优化策略和价值函数的参数。Actor定期从学习器中获取最新的策略。由于动作(action)的执行与学习被分离开来了,我们可以使用更多的actors来并行生成数据。由于我们正在训练的策略和行为策略(actors正在使用的)不是完全同步的,我们需要做off-policy 修正。
在训练时刻$t$,给定样本$(s_t, a_t, s_{t+1}, r_t)$,优化函数的参数$\theta$的loss为当前值与V-trace目标值之间L2 loss。V-trace 目标值定义为:
红色部分$\delta_i V$称作$V$的时间差异。$\rho_i = \min\big(\bar{\rho}, \frac{\pi(a_i \vert s_i)}{\mu(a_i \vert s_i)}\big)$与$c_j = \min\big(\bar{c}, \frac{\pi(a_j \vert s_j)}{\mu(a_j \vert s_j)}\big)$为重要性权重(截断式的)。$c_t, \dots, c_{i-1}$的乘积度量了时刻$i$时所观测到的时差$\delta_i V$对于时刻$t$时价值函数更新的影响。在on-policy的情况下,我们设置$\rho_i=1, c_j=1$,所以V-trace目标值就变成了n步的贝尔曼目标值。
$\bar{\rho}, \bar{c}$为截断常量,并且$\bar{\rho}\ge\bar{c}$。$\bar{\rho}$会影响我们价值函数最终收敛值,而$\bar{c}$会影响到训练的收敛速度。当$\bar{\rho} =\infty$(不截断)时,我们会收敛到目标策略的价值函数$V^\pi$;当$\rho$趋于0时,我们实际上测量了执行策略$V^\mu$;在某个中间值时,我们测量了策略$\pi$与$\mu$之间的某个策略。
值函数参数的更新方向为:
策略参数$\phi$通过策略梯度进行更新:
其中$r_t + \gamma v_{t+1}$为预测的Q值,基线值为$V_\theta(s_t)$。$H(\pi_\phi)$为策略的熵,用于加强探索。
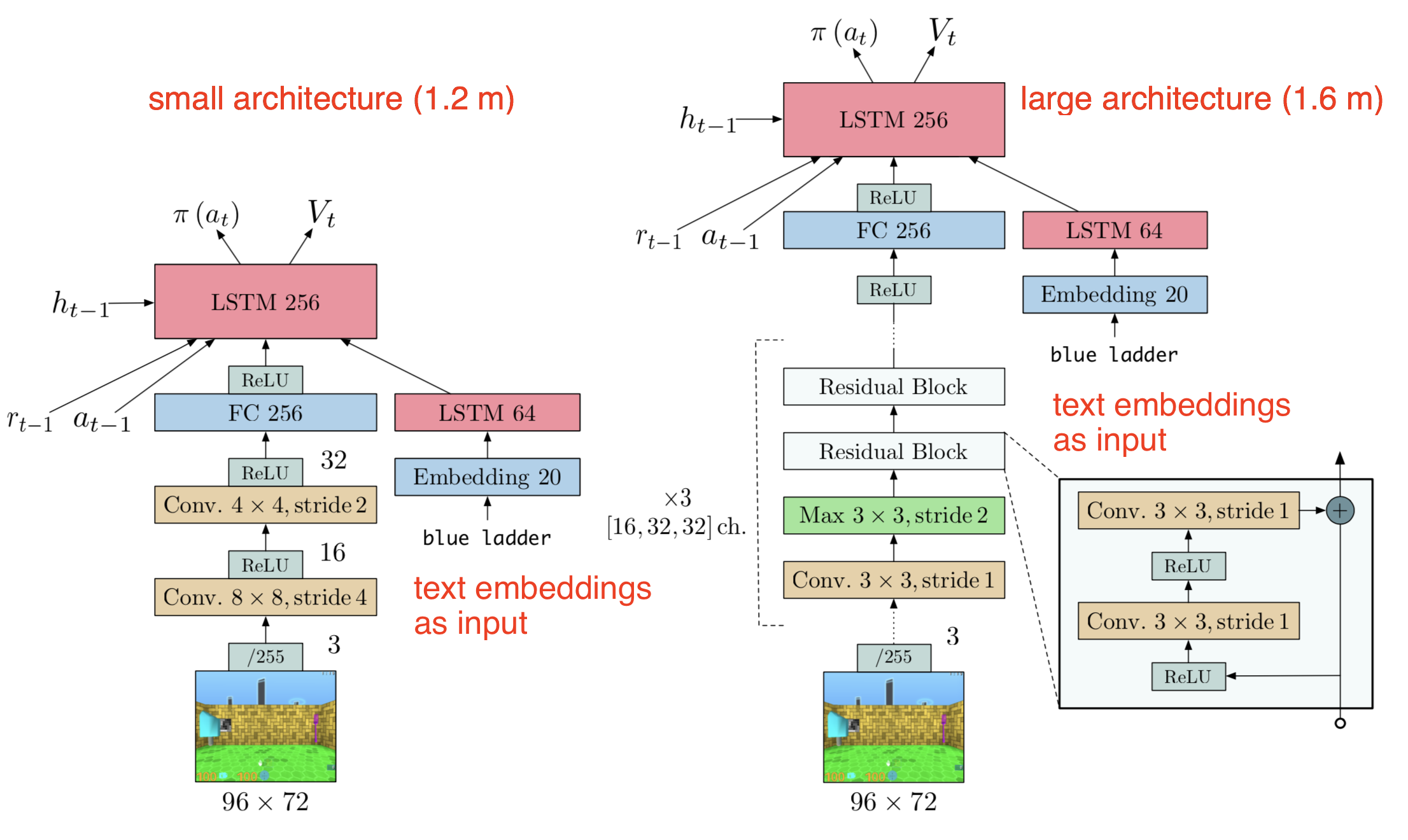
在论文的实验中,IMPALA被用于训练一个在多个任务上运行的执行体。实验使用了两个不同模型结构:一个影子模型(左)、一个深度残差模型(右)。
快速总结
在读完上述所有算法之后,我总结了一些点:
- 在保证偏差不变的前提下降低方差
- Off-policy 可以让我们更好地进行探索,并且可以提高数据效率
- 使用经验重放
- 目标网络要么定期冻结,要么比学习中的网络更新慢
- Batch Normalization
- 在reward中引入熵正则项
- Actor和Critic可以共享底层网络层,而在头部使用不同的网络层来分别输出策略和价值
- 可以使用确定性策略而不是随机性策略进行学习
- 对于策略更新的幅度进行限制
- 使用心得优化方法(如:K-FAC)
- 策略熵最大化可以加强探索(exploration)
- 尽量不要高估(overestimate)价值函数
- 如果想让策略网络与价值网络共享参数,好好想想能不能行
- 未完待续
使用如下方式引用本文:
@article{weng2018PG,
title = "Policy Gradient Algorithms",
author = "Weng, Lilian",
journal = "lilianweng.github.io/lil-log",
year = "2018",
url = "https://lilianweng.github.io/lil-log/2018/04/08/policy-gradient-algorithms.html"
}引用
[1] jeremykun.comMarkov Chain Monte Carlo Without all the Bullshit
[2] Richard S. Sutton and Andrew G. Barto.Reinforcement Learning: An Introduction; 2nd Edition. 2017.
[3] John Schulman, et al.“High-dimensional continuous control using generalized advantage estimation.”ICLR 2016.
[4] Thomas Degris, Martha White, and Richard S. Sutton.“Off-policy actor-critic.”ICML 2012.
[5] timvieira.github.ioImportance sampling
[6] Mnih, Volodymyr, et al.“Asynchronous methods for deep reinforcement learning.”ICML. 2016.
[7] David Silver, et al.“Deterministic policy gradient algorithms.”ICML. 2014.
[8] Timothy P. Lillicrap, et al.“Continuous control with deep reinforcement learning.”arXiv preprint arXiv:1509.02971 (2015).
[9] Ryan Lowe, et al.“Multi-agent actor-critic for mixed cooperative-competitive environments.”NIPS. 2017.
[10] John Schulman, et al.“Trust region policy optimization.”ICML. 2015.
[11] Ziyu Wang, et al.“Sample efficient actor-critic with experience replay.”ICLR 2017.
[12] Rémi Munos, Tom Stepleton, Anna Harutyunyan, and Marc Bellemare.“Safe and efficient off-policy reinforcement learning”NIPS. 2016.
[13] Yuhuai Wu, et al.“Scalable trust-region method for deep reinforcement learning using Kronecker-factored approximation.”NIPS. 2017.
[14] kvfrans.comA intuitive explanation of natural gradient descent
[15] Sham Kakade.“A Natural Policy Gradient.”. NIPS. 2002.
[16]“Going Deeper Into Reinforcement Learning: Fundamentals of Policy Gradients.”- Seita’s Place, Mar 2017.
[17]“Notes on the Generalized Advantage Estimation Paper.”- Seita’s Place, Apr, 2017.
[18] Gabriel Barth-Maron, et al.“Distributed Distributional Deterministic Policy Gradients.”ICLR 2018 poster.
[19] Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine.“Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor.”arXiv preprint arXiv:1801.01290 (2018).
[20] Scott Fujimoto, Herke van Hoof, and Dave Meger.“Addressing Function Approximation Error in Actor-Critic Methods.”arXiv preprint arXiv:1802.09477 (2018).
[21] Tuomas Haarnoja, et al.“Soft Actor-Critic Algorithms and Applications.”arXiv preprint arXiv:1812.05905 (2018).
[22] David Knowles.“Lagrangian Duality for Dummies”Nov 13, 2010.
[23] Yang Liu, et al.“Stein variational policy gradient.”arXiv preprint arXiv:1704.02399 (2017).
[24] Qiang Liu and Dilin Wang.“Stein variational gradient descent: A general purpose bayesian inference algorithm.”NIPS. 2016.
[25] Lasse Espeholt, et al.“IMPALA: Scalable Distributed Deep-RL with Importance Weighted Actor-Learner Architectures”arXiv preprint 1802.01561 (2018).
[26] Karl Cobbe, et al.“Phasic Policy Gradient.”arXiv preprint arXiv:2009.04416 (2020).
[27] Chloe Ching-Yun Hsu, et al.“Revisiting Design Choices in Proximal Policy Optimization.”arXiv preprint arXiv:2009.10897 (2020).

更多推荐